Some topics developed at SiMMaS
Skyrmions
Transport of skyrmions on racetracks. Analytical treatment with Thiele’s model
Magnetic skyrmions can be considered as magnetic bits due to their nanometric size and topologically protected stability. We have studied the dynamics of such skyrmions in racetrack geometries and, in general, in confined geometries. Analytical expressions for the trajectories of skyrmions in confined geometries (including long tracks and squared samples) when driven by polarized electric currents. The force exerted by the borders is derived as a function of the material parameters (anisotropy, Dzyaloshinskii-Moriya, and exchange constants) and incorporated in the equation of motion of the skyrmions.
More information: https://doi.org/10.1103/PhysRevB.94.184104
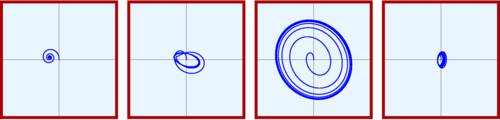
Transport of skyrmions on realistic racetracks. Granularity and temperature
Skyrmions, as as bits of information, that can be transported along nanoracetracks. However, temperature, defects, and/or granularity can produce diffusion, pinning, etc. These effects may cause undesired errors in information transport may be compromising the feasibility of the device. We have performed simulations of a realistic system where both the (room) temperature and sample granularity are taken into account. Key feasibility magnitudes, such as the success probability of a skyrmion traveling a given distance along the racetrack, are calculated. The model proposed is based on the Fokker–Planck equation resulting from Thiele’s rigid model for skyrmions.
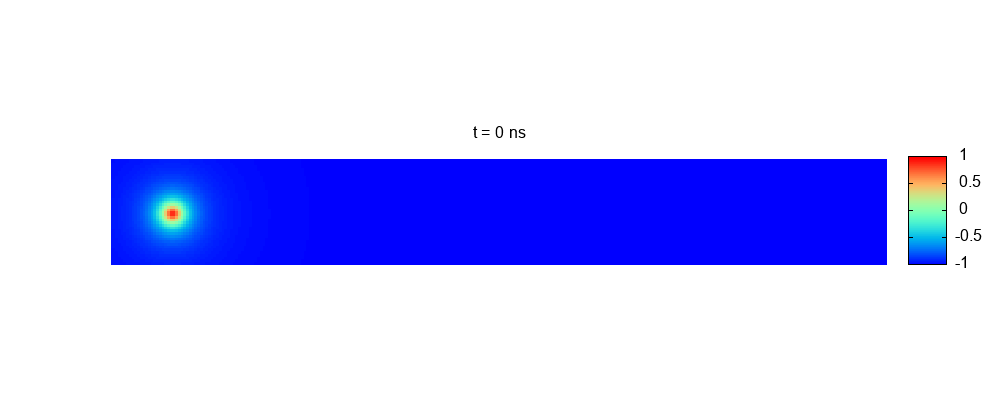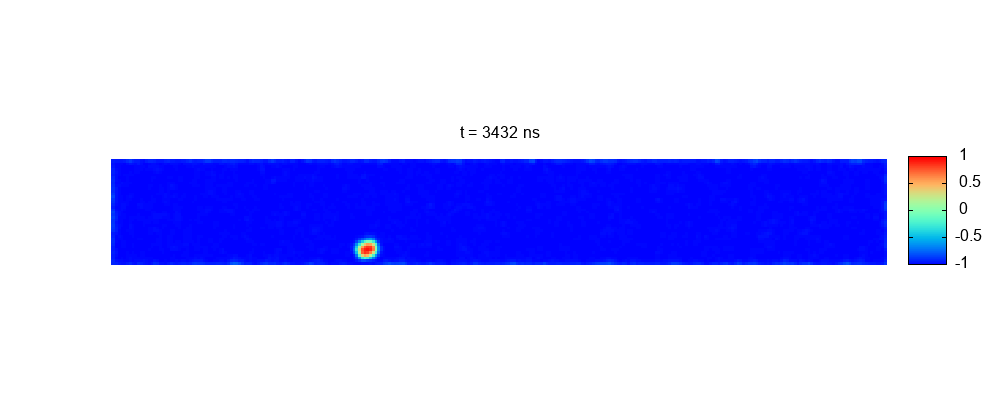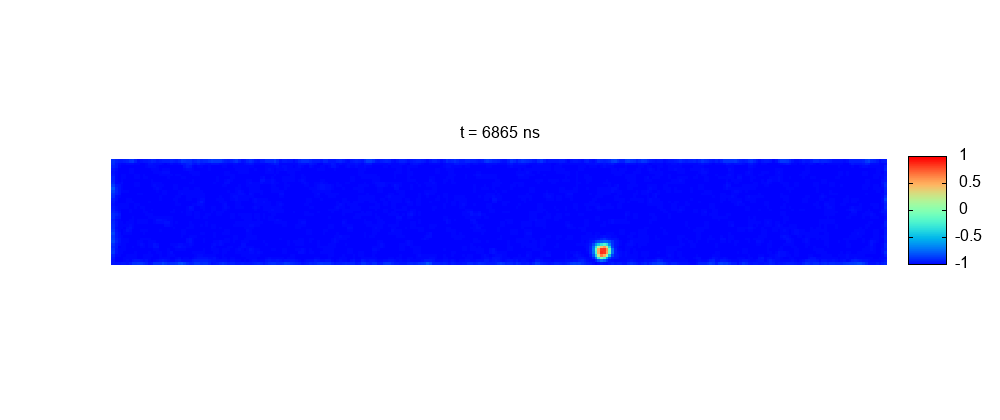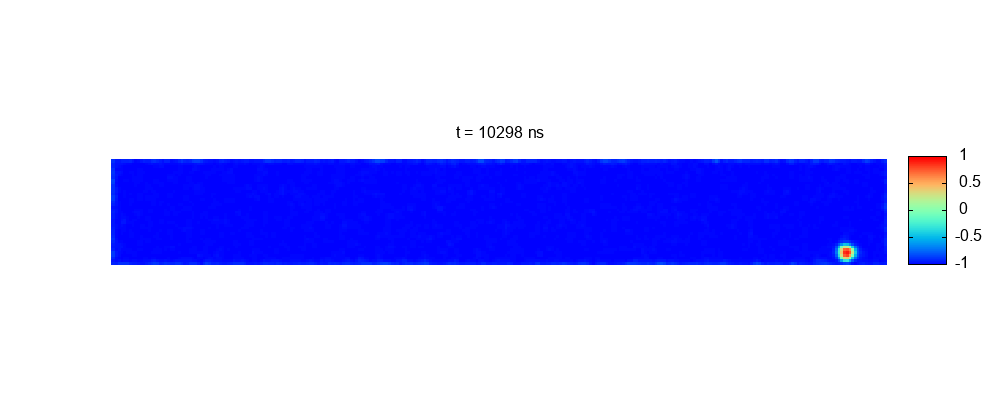
More information: https://pubs.rsc.org/en/content/articlelanding/2023/na/d3na00464c
Generation of skyrmions by template imprinting
Magnetic skyrmions are promising candidates as information carriers in new generation magnetic memories. The physical conditions for nucleating and stabilizing skyrmions depend largely on many parameters such as temperature or the type of materials. We have demonstrate how skyrmions can be imprinted in ultrathin ferromagnetic films, either individually and also in large numbers by bringing a magnetic nanostructured template close to the film.
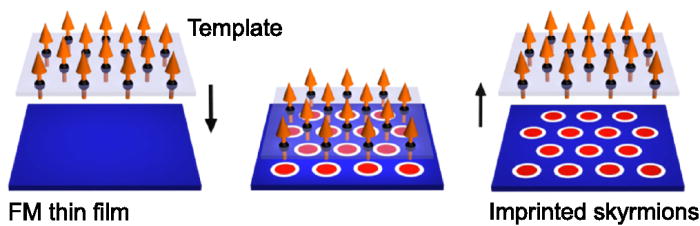
More Information: https://doi-org.are.uab.cat/10.1063/1.4932090
Hybrid Systems FM-SC
Magnetic multistates
We have developed simulations fro accounting for the interaction of a FM disk and a superconducting disk. The interaction is accounted for by solving simultaneously the Brown and London equations. We have discussed the effect of the different parameters on the results and some possible applications such as multivalued logic, storage, and skyrmionic metamaterials.
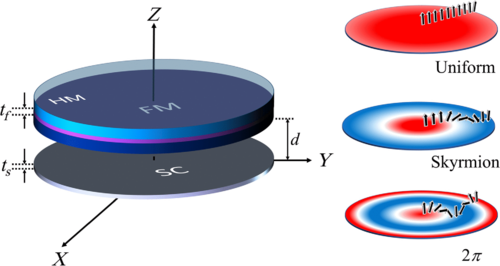
More information and details: 10.1103/PhysRevApplied.17.034069
Short questions/answers about this topics
What is a skyrmion?
A magnetic skyrmion is a topologically stable, swirling spin texture in a magnetic material. It consists of a localized region where the magnetization vector rotates continuously, forming a vortex-like structure. Skyrmions exhibit unique properties and have potential applications in magnetic storage, spintronics, and information processing.
Which is the Landau-Lifshitz-Gilbert equation?
The Landau-Lifshitz-Gilbert (LLG) equation is a fundamental equation in magnetism that describes the dynamics of a magnetization distribution in a magnetic material. It is given by:
dM/dt = –γ M x Heff + α M x (dM/dt)
M represents the magnetization distribution, t is time, γ is the gyromagnetic ratio, Heff is the effective magnetic field, α is the damping parameter, and dM/dt is the time derivative of the magnetization vector.
The first term on the right-hand side represents the precession of the magnetization around the effective magnetic field, while the second term accounts for the damping effect, which tends to align the magnetization with the effective field.

Page under construction