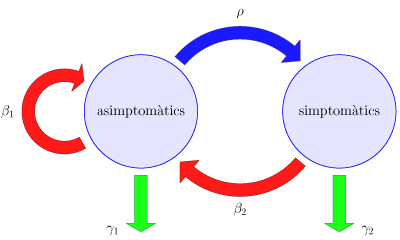
En la propagació de la covid-19 juga un paper molt important la presència d’individus asimptomàtics amb capacitat de transmissió. A més, especialment en la primera onada, només els simptomàtics eren detectats, de forma que una anàlisi de les dades ha de tenir en compte com a variables d’estat tant una població com l’altra.
Distingim doncs entre individus infectats asimptomàtics i individus infectats simptomàtics. Si suposem que un individu asimptomàtic té una probabilitat per unitat de temps \(\gamma_1\) de recuperar-se sense esdevenir malalt i una probabilitat \(\rho\), també per unitat de temps, de passar a la “categoria” de simptomàtic, mentre que produeix noves infeccions amb una taxa \(\beta_1\), llavors el nombre esperat d’infeccions que produirà abans de recuperar-se o bé emmalaltir ve donat per \(\beta_1/(\gamma_1+\rho)\).
El nombre de reproducció \(R_0\) serà almenys aquesta fracció i per tant l’epidèmia progressarà sempre que \(\beta_1>\gamma_1+\rho\), independentment de quins siguin els valors dels paràmetres (infectivitat \(\beta_2\) i taxa de recuperació \(\gamma_2\)) associats a la població simptomàtica.
En el model del diagrama, el nombre total esperat d’infeccions que produeix un nou infectat resulta \[R_{0,1} =\frac{\beta_1}{\gamma_1+\rho}+\frac{\rho}{\gamma_1+\rho}\frac{1}{\gamma_2}\beta_2,\] on el segon sumand és el nombre esperat d’infeccions que produirà un cop desenvolupi símptomes: la probabilitat que això passi, multiplicada pel temps esperat que romandrà en estat asimptomàtic \(1/\gamma_2\) i per la taxa \(\beta_2\) amb què produeix contagis.
En canvi, el nombre esperat d’individus simptomàtics que produeix un individu que ha començat a desenvolupar símptomes resulta \[R_{0,2} = \frac{\beta_2}{\gamma_2} \sum_{k = 0}^{\infty} \bigg( \frac{\beta_1}{\gamma_1+\rho } \bigg)^{k} \frac{\rho}{\gamma_1+\rho } = \frac{\beta_2}{\gamma_2}\frac{\rho}{\gamma_1+\rho-\beta_1}\] sempre que \(\beta_1 < \gamma_1 + \rho\), i infinit (!) en cas contrari. Efectivament, el primer factor és el nombre esperat d’asimptomàtics que produeix un individu simptomàtic (com abans) mentre que el sumand \(k\)-èsim del segon factor és el nombre esperat d’asimptomàtics “descendents en \(k\)-èsima generació” de cada asimptomàtic, multiplicat per la probabilitat d’esdevenir simptomàtic de cadascun d’aquests. Noti’s que el nombre esperat de “descendents de qualsevol generació” d’un individu asimptomàtic és infinit si \(\beta_1 \ge \gamma_1 + \rho\) .
És molt fàcil de veure que \(R_{0,1}\le 1\) si i només si \(R_{0,2}\le 1\), i, certament, també \(R_{0,1}>1\) si i només si \(R_{0,2}>1\): els dos factors de reproducció donen el mateix llindar per a la propagació de l’epidèmia.
Però la forma \(R_{0,2}\) és més adequada en termes del possible control basat només en l’aïllament dels casos detectats: una mesura d’aquest tipus disminueix \(\beta_2\) i exactament en la mateixa proporció \(R_{0,2}\), però no és tan clar l’efecte que té sobre \(R_{0,1}\).
Referència:
- J. M. Cushing, Odo Diekmann, 2016. The many guises of \(R_0\) (a didactic note). Journal of Theoretical Biology, 404: 295–302.