
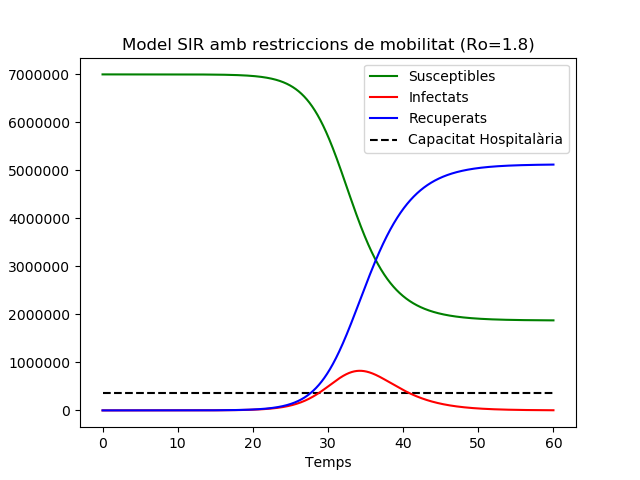
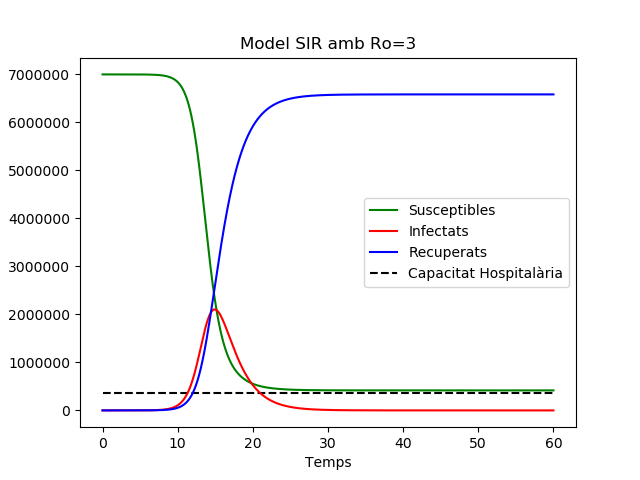
El model clàssic (simplificat) de Kermack-McKendrick (1927) descriu l’evolució del brot epidèmic d’una malaltia infecciosa on els naixements i les morts per causes naturals són negligits i per tant la mida de la població es manté constant. La població es divideix en 3 grups: individus Susceptibles (d’adquirir la malaltia), individus Infectats (poden transmetre la malaltia), i individus Recuperats (han superat la malaltia i són immunes). Les respectives poblacions varien amb el temps d’acord amb les equacions diferencials següents: \[ \begin{align} S'(t) &= -\beta I(t) S(t), \\ I'(t) &= \beta I(t) S(t) – \gamma I(t), \\ R'(t) &= \gamma I(t), \end{align} \] on \(\beta\) és la taxa de transmissió de la malaltia i \(\gamma\) és la taxa de recuperació.

El Nombre de reproducció bàsic \(R_0\) és el nombre esperat de noves infeccions produïdes per un individu infectat en una població d’individus susceptibles i estableix un llindar per a la propagació de l’epidèmia en el sentit que un brot epidèmic tindrà lloc si \(R_0>1\) mentre que la desigualtat estricta contrària garantirà que no hi haurà epidèmia.
Com que \(1/\gamma\) és la durada esperada de la malaltia i \(\beta\) és el número d’infeccions per unitat de temps que un infectat produeix, tenim que, per al model SIR, \(R_0=\beta N/\gamma\), on \(N\) és la població total (que al començament de l’epidèmia és tota susceptible).
Referència:
- W. O. Kermack, A. G. McKendrick, 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society A, 115: 700–721.