2021
Accounting for the instantaneous disorder in the enzyme–substrate Michaelis complex to calculate the Gibbs free energy barrier of an enzyme reaction
Romero-Téllez, S., Cruz, A., Masgrau, L., González-Lafont, À. & Lluch, J. M.
Phys. Chem. Chem. Phys., 2021 ,23, 13042-13054

Resum
Many enzyme reactions present instantaneous disorder. These dynamic fluctuations in the enzyme–substrate Michaelis complexes generate a wide range of energy barriers that cannot be experimentally observed, but that determine the measured kinetics of the reaction. These individual energy barriers can be calculated using QM/MM methods, but then the problem is how to deal with this dispersion of energy barriers to provide kinetic information. So far, the most usual procedure has implied the so-called exponential average of the energy barriers. In this paper, we discuss the foundations of this method, and we use the free energy perturbation theory to derive an alternative equation to get the Gibbs free energy barrier of the enzyme reaction. In addition, we propose a practical way to implement it. We have chosen four enzyme reactions as examples. In particular, we have studied the hydrolysis of a glycosidic bond catalyzed by the enzyme Thermus thermophilus β-glycosidase, and the mutant Y284P Ttb-gly, and the hydrogen abstraction reactions from C13 and C7 of arachidonic acid catalyzed by the enzyme rabbit 15-lipoxygenase-1.
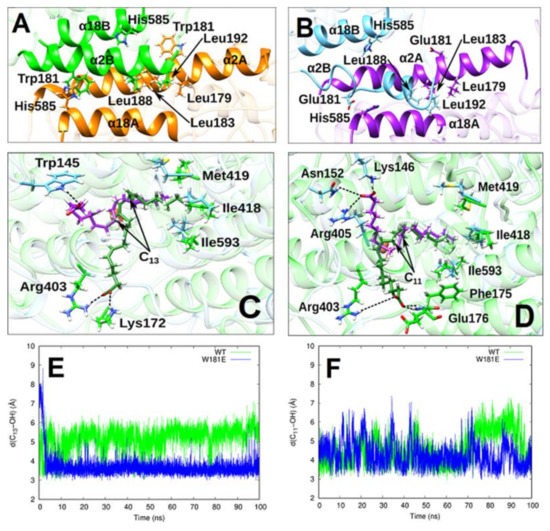
Conformational Heterogeneity and Cooperative Effects of Mammalian ALOX15
Ivanov, I.; Cruz, A.; Zhuravlev, A.; Di Venere, A.; Nicolai, E.; Stehling, S.; Lluch, J.M. ; González-Lafont, À.; Kuhn, H.
Int. J. Mol. Sci. 2021, 22(6), 3285
Resum
Arachidonic acid lipoxygenases (ALOXs) have been suggested to function as monomeric enzymes, but more recent data on rabbit ALOX15 indicated that there is a dynamic monomer-dimer equilibrium in aqueous solution. In the presence of an active site ligand (the ALOX15 inhibitor RS7) rabbit ALOX15 was crystalized as heterodimer and the X-ray coordinates of the two monomers within the dimer exhibit subtle structural differences. Using native polyacrylamide electrophoresis, we here observed that highly purified and predominantly monomeric rabbit ALOX15 and human ALOX15B are present in two conformers with distinct electrophoretic mobilities. In silico docking studies, molecular dynamics simulations, site directed mutagenesis experiments and kinetic measurements suggested that in aqueous solutions the two enzymes exhibit motional flexibility, which may impact the enzymatic properties.
2020
A protocol to obtain multidimensional quantum tunneling corrections derived from QM(DFT)/MM calculations for an enzyme reaction
Soler, J., González-Lafont, À. & Lluch Lopez, J. M.
Phys. Chem. Chem. Phys., 2020, 22, 27385-27393
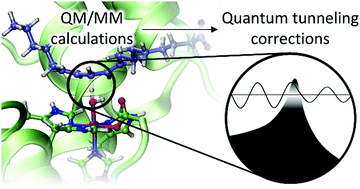
Resum
The significance of tunneling contributions to the rate constants of enzymatic reactions has been described at length using experimental evidence as well as theoretical computations. Within the frame of variational transition state theory (VTST), tunneling corrections are included using the so-called ground-state tunneling transmission coefficient. For the calculation of those enzymatic rate constants using the ensemble-averaged extension of VTST on QM/MM potential energy surfaces, the transmission coefficient at a given temperature is averaged over a set of coefficient values, each one obtained from an individual minimum energy path (MEP). However, the calculation of accurate QM/MM MEPs for tunneling calculations, also using a reliable QM method like DFT, is highly costly in enzyme models. For this reason, more affordable methodologies have been used. In this paper, we validate a feasible computational strategy to compute multidimensional tunneling corrections that describes better than cheaper alternatives the physics of the hydrogen abstraction from linoleic acid catalyzed by the enzyme 15-rLOX-1. Our recommendations to obtain better values of kinetic isotope effects and, especially, of rate constants are based on multidimensional small-curvature tunneling (SCT) coefficients derived from electrostatic embedding QM(DFT)/MM MEPs. The MEPs used must be calculated with a small enough step-size. Also, the number of gradients and Hessians along the reaction path must be checked to cover the whole tunneling region and to obtain converged adiabatic potential energy profiles. Distinguished reaction coordinates (DCPs) that are commonly used to describe enzyme reaction mechanisms are not adequate for tunneling calculations in such biological systems.